Comment mesurer la précision d’opérateurs de calculs d’attributs de reconnaissance de forme ?
1.introduction
L’état de l’art en reconnaissance de formes et de caractères propose un grand nombre d’études sur différents descripteurs de formes [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] mais elles sont toutes basées sur la théorie et l’expérimentation et aucune ne propose de comparaison basée sur la préservation de l’information, ce que nous appelons ici la précision. Alors que certains moments statistiques semblent efficaces pour faire de la reconnaissance de formes, du fait de leurs propriétés invariantes, nous ne savons pas à quels points ils conservent l’information utile et quelle quantité de bruit ils introduisent. Nous voulons aussi connaître la sensibilité de ces moments à la taille des images, l’épaisseur du trait ou encore l’origine du motif (fait à la main ou généré par ordinateur). Nous proposons ici une comparaison entre différents moments statistiques en utilisant une mesure de précision dans le cadre de la reconnaissance de caractères. Le reste de l’article est articulé comme suit : la section 2 détaille la théorie des moments sur lesquels nous avons travaillé, présentant aussi la transformée inverse. Dans la section 3 nous présentons notre méthode de mesure de la précision et dans la section 4, les données et le protocole expérimental avec lesquels nous avons travaillé. La section 5 présente nos résultats et nos commentaires. Nous concluons notre travail en section 6.
2.Les descripteurs de formes
2.1.Moments statistiques
Dans le domaine de la reconnaissance de formes, les moments statistiques sont largement utilisés [1] [2] [10]. Les moments cartésiens, centrés et de Zernike peuvent décrire une forme en un vecteur multidimensionnel utilisable par un classifieur. Ils décrivent le contenu d’une image par rapport à leurs axes, et sont conçus pour capturer à la fois l’information géométrique globale et détaillée à propos des formes. Nous choisissons de travailler avec de tels moments car ils présentent la possibilité d’en calculer la transformée inverse.
.
En considérant une image comme une fonction de distribution de densité cartésienne ![]() (fonction bidimensionnelle continue), Hu explique dans [37] et [38] que le
(fonction bidimensionnelle continue), Hu explique dans [37] et [38] que le ![]() moment cartésien de dimension 2 est défini en tant qu’intégrale de Riemman comme :
moment cartésien de dimension 2 est défini en tant qu’intégrale de Riemman comme :
(2.1.1) ![]()
.
Sous les conditions décrites par Shutler [8], nous savons quela séquence de moment ![]() est définie de manière unique par
est définie de manière unique par ![]() et inversement,
et inversement, ![]() est définie de manière unique par
est définie de manière unique par ![]() (théorème d’unicité).
(théorème d’unicité).
.
.
Ceci implique qu’une image peut être décrite et reconstruite si l’on utilise des moments d’un rang suffisamment élevé.
.
La version discrète de l’équation (2.1.1), pour une image constituée de pixels ![]() , donne :
, donne :
(2.1.2) 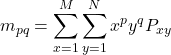
Où ![]() est le moment bidimensionnel Cartésien,
est le moment bidimensionnel Cartésien, ![]() et
et ![]() les dimensions de l’image et
les dimensions de l’image et ![]() la fonction de base.
la fonction de base.
.
En gardant les mêmes contraintes que pour les moments cartésiens, Shutler propose une extension aux moments centrés, la fonction (2.1.3) ![]() étant définie par :
étant définie par :![]()
Ainsi, l’équation (2.2.3) devient : (2.1.4) ![]()
.
Enfin, formulés à partir des travaux de Zernike [11] sous la forme complexe [9], les moments de Zernike (2.1.5) ![]() peuvent être exprimés comme :
peuvent être exprimés comme :![]()
Où ![]() ,
, ![]() dénote le complexe conjugué et
dénote le complexe conjugué et ![]() est le polynôme de Zernike exprimé en coordonnées polaires comme :
est le polynôme de Zernike exprimé en coordonnées polaires comme :
(2.1.6) ![]()
avec (2.1.7) (2.1.8) ![]() définis sur le disque unité,
définis sur le disque unité, ![]() et
et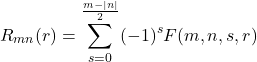
où![]()
2.2.Transformée inverse
Concernant la reconstruction, Shutler explique que si tous les moments ![]() (de l’ordre
(de l’ordre ![]() à l’ordre
à l’ordre ![]() ) d’une fonction
) d’une fonction ![]() et d’ordre
et d’ordre ![]() sont connus, il est possible d’obtenir la fonction continue
sont connus, il est possible d’obtenir la fonction continue ![]() dont les moments correspondent à ceux de la fonction originale
dont les moments correspondent à ceux de la fonction originale ![]() jusqu’à l’ordre
jusqu’à l’ordre ![]() .
.
.
En utilisant la décomposition en série de Taylor : (2.2.1) ![]()
.
Réduite en :
(2.2.2) ![]()
il faut calculer les coefficients constants (2.2.3) ![]() de façon à ce que les moments de
de façon à ce que les moments de ![]() correspondent à ceux de
correspondent à ceux de ![]() en supposant que l’image soit une fonction continue bornée par
en supposant que l’image soit une fonction continue bornée par ![]() . Pour obtenir ces limites, il est possible de normaliser les valeurs des pixels sur celles de moments cartésiens :
. Pour obtenir ces limites, il est possible de normaliser les valeurs des pixels sur celles de moments cartésiens :![]()
Ainsi, en substituant l’équation (2.2.1) dans (2.2.3) et en résolvant l’équation on obtient un ensemble linéaires dont le nombre est déterminé par l’ordre (2.2.4) ![]() de la reconstruction. Il faut alors les résoudre pour les coefficients
de la reconstruction. Il faut alors les résoudre pour les coefficients ![]() en inversant les matrices :
en inversant les matrices :![]()
Il suffit enfin de réintégrer les coefficients ![]() dans l’équation (2.2.1) pour reconstruire une approximation de l’image originale.
dans l’équation (2.2.1) pour reconstruire une approximation de l’image originale.
. |
De la même manière que nous avons calculé l’expression inverse des moments cartésiens, les moments centrés s’obtiennent à partir de :
(2.2.5) ![Rendered by QuickLaTeX.com \begin{equation*}M_{pq}=\sum_i\sum_jg_{ij}\frac{[(1-\bar{x})^{p+i+1}+(-1)^{p+i}(1+\bar{x})^{p+i+1}][(1-\bar{y})^{q+j+1}+(-1)^{q+i}(1+\bar{y})^{q+j+1}]}{(p+i+1)(q+j+1)}\end{equation*}](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-f2d11766784c8d4f57e467c84f823a23_l3.png)
Les moments centrés n’étant finalement qu’une extension des moments cartésiens permettant l’invariance à l’homothétie, les résultats obtenus après décomposition et reconstruction seront les mêmes.
.
Enfin, et en suivant la même méthode, nous pouvons reconstruire la fonction originale avec les moments de Zernike. Shutler rapporte même une méthode plus rapide, basée sur la condition d’orthogonalité [9] qui considère que si tous les moments cartésiens d’une fonction (2.2.6) ![]() sont connus jusqu’à un ordre
sont connus jusqu’à un ordre ![]() , il est alors possible de reconstruire une fonction discrète
, il est alors possible de reconstruire une fonction discrète ![]() dont les moments correspondent. Ce qui donne dans le cadre des moments de Zernike (exprimé par Khotanzad dans [6]) :
dont les moments correspondent. Ce qui donne dans le cadre des moments de Zernike (exprimé par Khotanzad dans [6]) :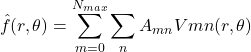
![]() pair et
pair et ![]() .
.
Après développement nous obtenons : (2.2.7) 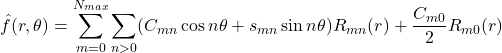
(2.2.8) (2.2.9) ![]() composant ainsi la partie réelle de
composant ainsi la partie réelle de ![]() comme :
comme :![]()
et ![]() la partie imaginaire :
la partie imaginaire :![]()
Un exemple de reconstruction après décomposition par moments de Zernike à plusieurs ordres est illustré par la Figure 2‑2. Le demi-disque obtenu à l’ordre 2 ainsi que le disque obtenu à l’ordre 3 sont liés à l’expression dans une base circulaire des moments de Zernike.
. | . |
Figure 2‑2 – Image originale et sa reconstruction avec les moments de Zernike à l’ordre 2, 3, 7, 9, 11, 13, 19, 25 et 49
2.3.PHENOMENE DE GIBBS
Nous pouvons constater sur les images présentées par la Figure 2‑1 et la Figure 2‑2, la présence d’ondulations autour de la forme à reconnaître du fait des dépassements des intervalles sur les discontinuités. Ceci est dû à l’incapacité pour une fonction continue de recréer une fonction discrète, qu’importe combien de termes finis de grand ordre, un dépassement de la fonction se produit ; c’est le phénomène de Gibbs [12]. Ce phénomène est un dépassement (ou ringing) des séries de Fourier et autres séries de fonctions sur des simples discontinuités, qui augmente jusqu’à diluer totalement l’information utile.
.
Ceci peut être expliqué en termes de séries de Fourier : (2.3.1) (2.3.2)
Soit ![]() une fonction continue intégrable définie par parties, périodique de période
une fonction continue intégrable définie par parties, périodique de période ![]() .
.
Supposons qu’à certains points ![]() les limites gauche
les limites gauche ![]() et droite
et droite ![]() de la fonction
de la fonction ![]() diffèrent d’une valeur non nulle de coupure
diffèrent d’une valeur non nulle de coupure ![]() :
:![]() . Pour chaque entier
. Pour chaque entier ![]() , soit
, soit ![]() la
la ![]() th série de Fourier partielle :
th série de Fourier partielle :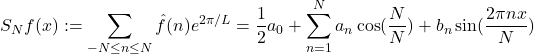
où ![]() ,
,![]() ,
,![]() sont les coefficients de Fourier. Si
sont les coefficients de Fourier. Si ![]() est une séquence de nombres réels convergeant vers
est une séquence de nombres réels convergeant vers ![]() comme
comme ![]() , et si la valeur de coupure
, et si la valeur de coupure ![]() est positive alors :
est positive alors :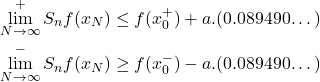
Notons que si la valeur de coupure est négative, il faut échanger les limites supérieures et inférieures, ainsi que les termes d’égalité.
3.mesure de la precision
La mesure que nous cherchons à estimer correspond à la quantité d’information qui est prise en compte par l’attribut. Cette mesure correspond au pourcentage d’information conservé par l’attribut par rapport à l’information complète. Dans notre cas, cette mesure s’obtient par le biais d’une mesure de distance entre l’objet original et l’objet reconstruit. Toute la difficulté provient de l’application de la mesure de distance à utiliser qui diffère selon la nature de l’information extraite par l’opérateur de calcul de l’attribut. Dans le cas d’un opérateur de quantification couleur, la distance s’appuiera forcément sur la perte de complexité obtenue, estimée par une somme de différences couleurs établies dans un espace couleur adapté (id. ΔE ou ΔE2000 dans l’espace CIE La*b*). Les différences étant calculées entre la couleur du pixel de l’image originale ![]() et le pixel de l’image quantifiée
et le pixel de l’image quantifiée ![]() et la somme conduite sur toutes les positions
et la somme conduite sur toutes les positions ![]() de l’image.
de l’image.
.
Dans l’exemple qui nous intéresse, nous nous attachons à des objets binaires de couleur noire (valeur nulle) sur fond blanc. L’objet reconstruit à partir des moments que nous utilisons n’est en revanche pas binaire, mais en niveaux de gris à cause de la formulation héritée du domaine continu. La binarisation de l’objet est donc un étage supplémentaire à prévoir avant le calcul de la distance entre objet reconstruit et original.
3.1.QUELLE FONCTION DE DISTANCE ?
Soient deux images binaires ![]() et
et ![]() définies sur un même support spatial de taille
définies sur un même support spatial de taille ![]() pixels avec
pixels avec ![]() et
et ![]() nuls pour tous les pixels de l’objet représenté sur l’image originale (par voie de conséquence,
nuls pour tous les pixels de l’objet représenté sur l’image originale (par voie de conséquence, ![]() pour tous les pixels du fond).
pour tous les pixels du fond).
Les premières fonctions de distance auxquelles nous pourrions penser sont les métriques de type Minkowski :
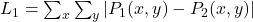 ,
,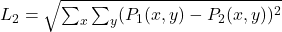 ,
,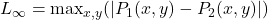 ,
,
les métriques en ![]() étant notamment bien adaptées dans notre cas où
étant notamment bien adaptées dans notre cas où ![]() et
et ![]() sont binaires.
sont binaires.
La formulation à retenir pour notre estimation de la précision doit être normalisée entre 0 et 1 si nous souhaitons l’exploiter dans des formalismes tels que celui du modèle des croyances transférables.
La première mesure de précision proposée est alors : (3.1.1) 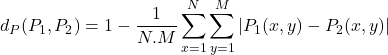
Cette métrique apparemment simple peut masquer les difficultés posées par le choix d’une bonne formulation. Bien évidemment, nous en avons formulé plusieurs et recherché différentes propositions dans la littérature. Nous pourrions, par exemple, dans le cadre d’objets binaires, proposer une expression du type : (3.1.2) ![]()
où ![]() correspond à l’inverse booléen de
correspond à l’inverse booléen de ![]() et
et ![]() le nombre de pixels de
le nombre de pixels de ![]() qui sont nuls donc appartenant à l’objet représenté.
qui sont nuls donc appartenant à l’objet représenté.
Cette formulation est séduisante car uniquement centrée sur l’objet binaire original et reconstruit. La normalisation par le nombre de pixels utiles de l’objet représenté dans l’image originale lui confère en plus une meilleure sensibilité aux évolutions des opérateurs en amont. Cependant, si nous posons complètement le problème en considérant que l’image originale ![]() est composée de
est composée de ![]() pixels de valeur nulle (donc
pixels de valeur nulle (donc ![]() pixels de valeurs non nulle) et que l’image reconstruite est composée de
pixels de valeurs non nulle) et que l’image reconstruite est composée de ![]() pixels de valeur nulle et
pixels de valeur nulle et ![]() pixels de valeur non nulle (
pixels de valeur non nulle (![]() ). Les différents cas de figure possibles sont représentés dans le tableau suivant.
). Les différents cas de figure possibles sont représentés dans le tableau suivant.
. |
| |
Ce tableau permet de comparer les quantités ![]() et
et ![]() , nombre de pixels de l’image reconstruite présentant la bonne valeur avec les erreurs de reconstruction
, nombre de pixels de l’image reconstruite présentant la bonne valeur avec les erreurs de reconstruction ![]() et
et ![]() .
.
.
Dans le cas de la métrique issue de la distance de Minkowski d’ordre 1 : (3.1.3) ![]()
.
Si nous analysons différents cas de figure :
- Une reconstruction parfaite (
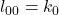 et
et 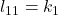 ) :
) : 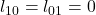
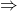
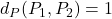 ,
, - une reconstruction inversée (
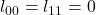 ) :
) : 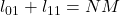
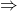
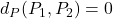 ,
, - le pire cas d’une reconstruction d’une image blanche (
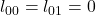 ) :
) : 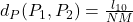 ,
, - le pire cas d’une reconstruction d’une image noire (
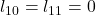 ) :
) : 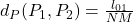 ,
,
la dynamique de la mesure est comme évoquée précédemment fonction des ratios ![]() dépendant de la taille des images considérées.
dépendant de la taille des images considérées.
Dans le cas de la seconde métrique, l’expression de la formule pour le cas proposé devient : (3.1.3) ![]()
Ce qui donne, en reprenant les mêmes cas de figure que précédemment :
- Une reconstruction parfaite (
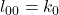 et
et 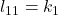 ) :
) : 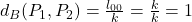 ,
, - une reconstruction inversée (
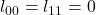 ) :
) : 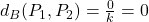 ,
, - le pire cas d’une reconstruction d’une image blanche (
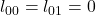 ) :
) : 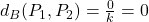 ,
, - le pire cas d’une reconstruction d’une image noire (
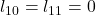 ) :
) : 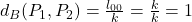 ,
,
la dynamique de la mesure est ici supérieure à la première puisqu’égale à ![]() avec
avec ![]() (par définition l’objet n’est pas une image noire).
(par définition l’objet n’est pas une image noire).
Cependant, comme le montre la séquence de cas, la mesure ![]() va avoir tendance à surévaluer la mesure lorsque l’image reconstruite va tendre vers un objet uniformément noir.
va avoir tendance à surévaluer la mesure lorsque l’image reconstruite va tendre vers un objet uniformément noir.
Malgré donc une apparente simplicité de la formulation, l’expression ![]() prend en compte tous les paramètres nécessaires : la partie de l’objet similaire et la partie du fond similaire entre les deux objets, et finalement, la dynamique plus faible n’est due qu’à une prise en considération de plus d’informations dans la double somme.
prend en compte tous les paramètres nécessaires : la partie de l’objet similaire et la partie du fond similaire entre les deux objets, et finalement, la dynamique plus faible n’est due qu’à une prise en considération de plus d’informations dans la double somme.
3.2.BINARISATION DE L’IMAGE RECONSTRUITE
Les images reconstruites à partir des différents moments ne sont pas binaires mais continues discrétisées. Pour appliquer les mesures de distance il convient auparavant de binariser les images reconstruites. Comme nous avons pu le constater dans la première partie de ce chapitre, le niveau d’intensité moyen de l’image reconstruite peut varier de façon importante (Figure 2‑1 et Figure 2‑2), l’utilisation d’un seuil fixé a priori n’est donc pas envisageable.
.
Cette question est pour nous une des premières applications de la mesure de la précision locale pour déterminer le seuil de binarisation idéal. Nous avons choisi de boucler selon ce critère de précision un système cherchant le seuil idéal de binarisation (voir Figure 3‑1).
Ce schéma classique de système en boucle fermée laisse libre court au choix de l’algorithme d’établissement du nouveau seuil (tracking, dichotomie etc.). Les résultats qui sont présentés par la suite correspondent à un algorithme de poursuite simple. Ils montrent selon toute vraisemblance un accroissement de la précision jusqu’à un seuil idéal, puis une décroissance une fois ce seuil dépassé.
.
Les figure 3‑2, 3‑3 et 3‑4 représentent chacune trois exemples de l’application de cette technique de seuillage. On retrouve en haut l’individu original et sa reconstruction, et en bas la reconstruction après seuillage accompagnée de l’évolution de la précision en fonction de la valeur du seuil. Nous avons fait le choix de prendre à chaque fois deux individus très différents au niveau de leur forme et de leur complexité pour illustrer la différence de comportement de la précision. Chaque figure est associée à une famille de moments, respectivement les moments cartésiens, les moments centrés et les moments de Zernike.
.
Nous constatons en premier lieu sur ces figures, et ce résultat était attendu selon la théorie, que les images obtenues après reconstruction sont strictement identiques que l’on utilise les moments cartésiens ou les moments centrés. Ce phénomène est dû au fait que les bases de décomposition sont strictement identiques, la seule différence étant que les moments centrés sont une réécriture des moments Cartésiens prenant en compte les transformations géométriques de type translation. Il est donc en effet logique, pour une même image donnée, d’obtenir strictement la même reconstruction.
.
Notons également que, comme attendu, la précision évolue effectivement en même temps que la valeur du seuil, jusqu’à un optimal au-delà duquel elle décroît. Il existe cependant des différences dans l’évolution de la précision. D’une part, avec les moments cartésiens (et centrés), l’optimum est atteint plus rapidement pour le caractère alpha que pour le rectangle noir. L’information utile (i.e. les pixels décrivant la forme) étant mieux répartie pour un rectangle plein que pour un caractère au trait fin et de forme complexe, elle subit de fait moins fortement l’influence du phénomène de Gibbs. Nous constatons d’ailleurs très bien sur l’image reconstituée que le rectangle semble plus compact sur un fond plus clair.
Notons d’autre part l’évolution de la précision au-delà de l’optimum. Celle-ci chute brutalement avec les moments cartésiens (et centrés), tandis que la décroissance est plus douce avec les moments de Zernike. Ceci semble indiquer une meilleure conservation de l’information pour cette famille de moments, ainsi qu’une plus faible sensibilité au bruit induit par le phénomène de Gibbs.
.
Cependant, en s’attardant sur la valeur des optimums, en fonction de la forme ou de la famille de moments utilisés, nous nous apercevons que ceux obtenus à l’aide des moments cartésiens (ou centrés) sont meilleurs que ceux obtenus par les moments de Zernike. Cela peut être dû à une trop forte sensibilité de la méthode de calcul de la précision (et du seuillage) au bruit généré par la reconstruction. Une meilleure conservation de l’information originale par les moments Cartésiens (ou centrés) peut également en être à l’origine. Trier [10] et Shutler [8] indiquent bien que chaque famille de moments induits des déformations géométriques : les moments de Zernike ayant tendance à favoriser les arrondis (du fait de leur écriture complexe) à l’inverse des moments Cartésiens qui eux favorisent les formes angulaires.
4.donnees et protocole
Nous travaillons sur des images issues de la base MNIST, des images issues de notre propre collection (4000 caractères grecs, la moitié manuscrite, l’autre générée par traitement de texte sur différentes polices et tailles) et des images issues de la base GREC’05.
.
Dans l’optique de vérifier si la quantité d’information utile en fonction de la taille du symbole est importante, un changement d’échelle est appliqué sur chaque image de 1 à 3 (avec un pas de 0.1). Tous les moments statistiques sont calculés de l’ordre 1 à 35, afin de prendre en compte la dilution de l’information utile dans l’information générée par la reconstruction. Nous utilisons également un algorithme de dilatation pour obtenir quatre nouvelles images (1x, 2x, 3x and 4x) afin de procéder à un changement d’épaisseur de trait en compensation de la différence d’épaisseur entre les symboles manuscrits et ceux générés artificiellement.
.
Notons enfin la particularité des moments de Zernike : l’analyse et la reconstruction, ces moments s’inscrivant dans une base complexe, se font dans un cercle ; il existe alors une zone qui n’est jamais traitée, et visible en noir sur les figures vues précédemment. Afin de compenser ce phénomène, toute image analysée est d’abord recopiée au centre d’une image plus grande, de façon que l’image originale soit inscrite dans le cercle d’analyse. Ensuite, pour la comparaison des données, la mesure de la précision ne se fera que dans une fenêtre centrée, de la taille de l’image d’origine.
Toutes les figures représentent l’évolution de la précision pour les 3 familles de moments, en fonction de l’ordre du moment. La Figure 5‑1 concerne les caractères manuscrits de notre propre base et les reproductions manuscrites des symboles de la base GREC’05 à gauche. Sur la droite, nous trouvons la précision obtenue en utilisant les symboles de la base de test GREC’05 et les caractères grecs générés en utilisant un logiciel de traitement de texte. La Figure 5‑2 a été générée en utilisant tous les caractères et symboles manuscrits ainsi que les images obtenues en utilisant les différentes dilatations, et la Figure 5‑7 a été générée à partir de la base MNIST et de différents niveaux de zoom, montrant l’impact du changement d’échelle.
.
La première observation est que les moments cartésiens et centrés donnent toujours sensiblement les mêmes niveaux de précision, ce qui est un comportement logique étant donné que la différence entre les deux écritures, comme nous l’avons vu plus haut, ne réside que dans une translation qui présente une meilleure invariance mais qui n’influe pas sur l’information conservée. De plus, les objets analysés ici sont à peu près centrés dans l’imagette qui les représente, ce qui rend caduc l’intérêt des moments centrés.
5.1.INFLUENCE DE L’ASPECT MANUSCRIT
Entre les parties gauche et droite de la Figure 5‑1, la différence est la précision maximale pour les moments de Zernike, cartésiens et centrés. Pour les caractères générés et les symboles, les moments non orthogonaux préservent plus d’information que les moments de Zernike, et donnent la possibilité de recréer quasi parfaitement l’image originale en utilisant un ordre entre 15 et 20. Pour les documents manuscrits, les moments de Zernike donnent les meilleurs résultats. Ceci peut être expliqué d’une part par l’épaisseur du trait (les caractères générés sont plus épais que les manuscrits), et d’autre part par le fait que les symboles générés sont plus « angulaires » que les manuscrits. En effet, et comme l’expliquent Trier [10] et Shutler [8] du fait de leur base orthogonale et de leur forme complexe, les moments de Zernike semblent plus adaptés aux formes arrondies, telles que les caractères et les symboles manuscrits.
.
Afin de valider notre hypothèse sur l’épaisseur du trait, nous avons observé l’évolution de la précision en fonction de l’ordre des moments, pour les images d’origines dilatées plusieurs fois.
5.2.INFLUENCE DE L’EPAISSEUR DU TRAIT INITIAL
Observons en premier lieu que pour la Figure 5‑2, la précision maximale obtenue avec les moments de Zernike n’augmente pas avec l’épaisseur du trait.
.
En ce qui concerne les moments orthogonaux (moments cartésiens et moments centrés), nous pouvons voir que plus le trait est épais, meilleure est la précision (inférieure à 0.9 sans dilatation, supérieure à 0.9 après dilatation x4).
.
Notons sur les figures 5‑3, et 5‑4 que les caractères et symboles manuscrits sont réalisés avec de feutres ou stylos à pointe relativement fine (trait de contour fin). Notons aussi, sur les figures 5‑5 et 5‑6, que les traits des caractères et symboles générés artificiellement sont eux plus épais.
.
En commentaire de la Figure 5‑1 nous émettions l’hypothèse que les différences de précisions obtenues pour les caractères et symboles manuscrits, par rapport aux caractères dits ”artificiels”, pouvaient s’expliquer par l’influence de l’épaisseur du trait. Les résultats que nous venons d’exposer renforcent cette hypothèse : l’information utile sera d’autant mieux conservée par les moments cartésiens (et centrés) que le trait du caractère sera épais, alors que les moments de Zernike ne semblent pas sensibles à ce paramètre.
5.3.INFLUENCE DU CHANGEMENT D’ECHELLE
Constatons d’abord que pour les résultats obtenus à l’échelle 1, des différences de comportement notable apparaissent entre les moments cartésiens et les moments centrés. Ce phénomène s’explique par le fait que les images de la base MNIST sont petites (20×20 pixels) ; l’information utile (les pixels appartenant à la forme d’origine) se retrouve rapidement diluée dans le bruit généré par la reconstruction (interpolations, phénomène de Gibbs, seuillage etc.). Même si en termes de coût de calcul, il peut sembler intéressant de travailler sur des images de la plus petite taille possible, nous voyons très bien qu’une certaine stabilité de l’évolution de la précision en fonction de l’ordre s’installe à partir d’un changement d’échelle de 2.
.
Observons aussi la courbe en dents de scie de la précision pour les petites échelles, qui se stabilise ensuite pour des échelles plus élevées. Notons également une variation de l’ordre maximal avant la chute de la précision pour les moments de Zernike. Ceci est attendu du fait que l’algorithme d’échelle génère de l’information inutile. Du fait de la nature corrélée des moments non orthogonaux, chaque moment ne porte pas que sa propre contribution à l’information individuelle. Ceci dissout l’information utile pour les ordres de moment les plus grands. Même si accroître le nombre de pixels utiles n’améliore pas significativement la précision, cela contribue tout de même à en stabiliser l’évolution.
.
Finalement, nous pouvons voir sur toutes les figures que la précision augmente jusqu’à chuter fortement, pour toutes les familles de moments. Ceci est dû, comme nous l’avons vu précédemment, au phénomène de Gibbs et au fait que les transformées inverses et la reconstruction se fassent avec des fonctions continues pour estimer des fonctions discrètes : un dépassement de la fonction fini par se produire.
La sensibilité à l’ordre, épaisseur et taille peut être expliquée par la dilution de l’information utile dans l’information totale (partiellement expliquée par la malédiction de la dimension), et par le phénomène de Gibbs. La théorie le prévoie et nous le voyons clairement dans nos résultats. Nous ne conseillons d’ailleurs pas de changer l’échelle de l’image à cause du bruit induit par ce genre de méthode.
.
Les moments centrés et cartésiens semblent être les méthodes les plus précises mais elles sont également les plus sensibles aux transformations géométriques, et c’est un réel problème concernant l’écriture manuscrite et les documents techniques complexes. Ces moments demandent cependant un très faible coût de calcul comparé aux moments de Zernike. D’une part, sachant l’ordre optimal (entre 10 et 22), nous supposons qu’il est possible de proposer un traitement de reconnaissance utilisant à la fois les moments statistiques et de l’information exogène (par exemple, de l’information concernant les transformations géométriques obtenues grâce aux différents invariants). D’autre part, nous retrouvons ici tout l’intérêt de la chaîne de traitement et de ses bouclages, permettant de combiner les différents types de vecteurs de moments d’ordre le plus faible possible pour une précision maximale et une sensibilité minimale aux transformations géométriques. Dans tous les cas, le choix se faisant selon la connaissance de l’évolution de la précision, impliquant un processus d’apprentissage en amont.
.
A propos des différences de comportement de la précision entre les caractères manuscrits et ceux générés, il ne doit pas exister d’influence de la géométrie des symboles (comme l’angularité), seule l’épaisseur compte. Dans ce cas, il doit être possible d’ajouter de l’information sur l’individu à reconnaître (pour un faible coût de calcul) et de décider d’utiliser une dilatation si c’est un symbole manuscrit.
.
Il pourrait être finalement intéressant d’analyser les effets de la précision si nous utilisons ensuite une étape de classification après le calcul des moments et de trouver une relation entre la quantité d’information préservée et les performances de reconnaissance. D’autres méthodes de similarité doivent également être testées, comme d’autres métriques de distances, de comparaison entre les formes d’origine et celle reconstituée (c’est à dire une analyse au niveau de la forme et non pas une au niveau des pixels) ou alors en se basant sur des notions comme l’entropie de l’image.
.
Il est ainsi possible de choisir le descripteur de forme le plus approprié, en prenant en compte la précision, selon une connaissance a priori du document en cours d’analyse.
.
Références
[1] | S. Belkasim, M. Shridhar and A. Ahmadi, « Pattern recognition with moments invariants: A comparative study and new results, » Pattern Recognition, pp. 1117-1138, 1991. |
[2] | S. Belkasim, M. Shridhar and A. Ahmadi, « Corrigendum, » Pattern Recognition, p. 377, 1993. |
[3] | H. Blum, « A transformation for extracting new descriptions of shape, » Models for the Perception of Speech and Visual Form, pp. 362-380, 1967. |
[4] | M.-K. Hu, « Pattern recognition by moments invariants, » in Proc. IRE (correspondence), 1961. |
[5] | M.-K. Hu, « Visual pattern recognition by moment invariants, » IRE Trans. on Information Theory, pp. 179-187, 1962. |
[6] | A. Khotanzad and Y. Hong, « Invariant image recognition by Zernike moments, » IEEE Trans. Pattern Anal. Mach. Intell., pp. 489-497, 1990. |
[7] | A. Khotanzad and Y. Hong, « Rotation invariant image recognition using features selected via a systematic method, » Pattern Recognition, pp. 1089-1101, 1990. |
[8] | J. Shutler, « Statistical Moments, » [Online]. Available: http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/SHUTLER3/CVonline_moments.html. |
[9] | M. Teague, « Image analysis via the general theory of moments, » Journal of the Optical Society of America, pp. 920-930, 1979. |
[10] | Ø. Trier, A. Jain and T. Taxt, « Feature extraction methods for character recognition – a survey, » Pattern Recognition, pp. 405-410, 1997. |
[11] | F. Zernike, « Beugungstheorie des schneidenverfahrens und seiner verbesserten form, der phasenkontrastmethode (diffraction theory of the cut procedure and its improved form, the phase contrast method), » Physica, vol. 1, pp. 689-704, 1934. |
[12] | N. K. Sinha, « Chapter 3, » in Linear Systems, Wiley, 1991. |
.
.
